Indhold

• Steps
• Tips

Matematikere og grafikprogrammerere har ofte brug for at finde vinklen mellem to vektorer. Heldigvis kræver formlen, der bruges til at beregne denne vinkel, ikke andet end et simpelt skalarprodukt. Selvom begrundelsen bag denne formel er lettere at forstå, når du bruger to-dimensionelle vektorer, kan vi let tilpasse den til vektorer med et hvilket som helst antal komponenter.

Steps

Del 1 af 2: Beregn vinklen mellem to vektorer

1. 

   Identificer de to vektorer. Skriv alle de kendte oplysninger om de to vektorer ned. Med henblik på denne tutorial antager vi, at du kun kender vektorerne med hensyn til deres dimensionelle koordinater (også kaldet komponenter). Hvis du allerede kender modul eller standard af disse vektorer (det vil sige deres længde), kan du springe over nogle af trinnene nedenfor.
   • Eksempel: Vi overvejer de to-dimensionelle vektorer = (2,2) og = (0,3). Disse to vektorer kan omskrives som = 2jeg + 2j e = 0jeg + 3j = 3j.
   • Selvom vores eksempel bruger to todimensionelle vektorer, kan vi anvende følgende instruktioner på vektorer med et hvilket som helst antal komponenter.

2. 

   
   
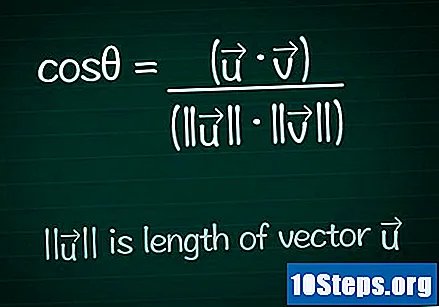
   Skriv kosinusformlen. For at finde værdien af ​​vinklen θ mellem to vektorer, skal vi først beregne kosinus for den vinkel. Du kan søge og finde ud af formlen i detaljer eller blot skrive den som den er nedenfor:
   • cosθ = (•) / (|||| ||||)
   • |||| repræsenterer modul (eller længde) af vektoren ".
   • • repræsenterer skalar produkt (eller internt produkt) af de to vektorer.

3. 

   
   
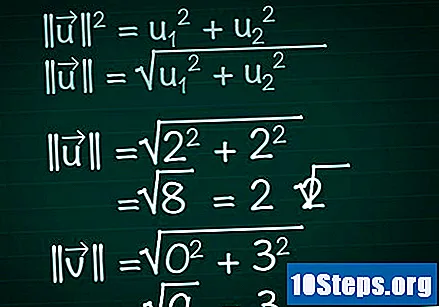
   Beregn modulen for hver vektor. Forestil dig en højre trekant dannet af komponenten x af en vektor, dens komponent y og selve vektoren. I denne trekant spiller vektoren hypotenusens rolle; Derfor vil vi bruge Pythagorean-sætningen for at finde dens længde. Som et resultat er denne formel let anvendelig til vektorer med et hvilket som helst antal komponenter.
   • || u || = u₁ + u₂. Hvis vektoren har mere end to komponenter, skal du bare fortsætte med at tilføje + u₃ + u₄ +...
   • Derfor skal vi til en to-dimensionel vektor || u || = √ (u₁ + u₂).
   • I vores eksempel | |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   Beregn det skalære produkt mellem de to vektorer. Du skal allerede kende metoden til at multiplicere vektorer, også kaldet skalar produkt. For at beregne det skalære produkt af to vektorer med hensyn til deres komponenter multiplicerer vi komponenterne i samme retning med hinanden og tilføjer derefter resultaterne af disse produkter.
   • Hvis du arbejder med computergrafikprogrammer, skal du først besøge afsnittet "Tips", før du fortsætter.
   • I matematiske termer, • = u₁v₁ + u₂v₂, hvor u = (u₁, u₂). Hvis din vektor har mere end to komponenter, skal du bare fortsætte med at tilføje + u₃v₃ + u₄v₄...
   • I vores eksempel er • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Dette er værdien af ​​det skalære produkt mellem vektorerne og.

5. 

   Udskift disse resultater i kosinusformlen. Husk, cosθ = (•) / (|||| || ||). Vi har allerede beregnet skalarproduktet og modulet for de to vektorer. Lad os nu erstatte disse værdier i formlen og beregne vinkinenes kosinus.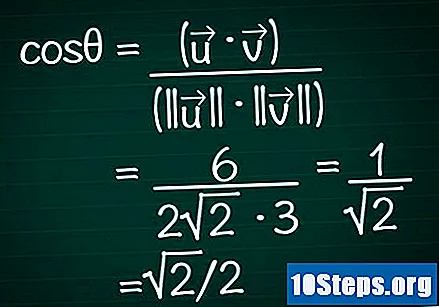
   • I vores eksempel er cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Find vinklen baseret på din kosinus.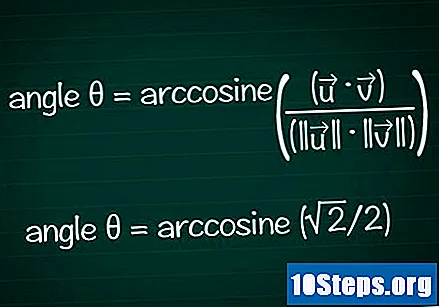
   Brug lommeregnerens bue- eller cos-funktion til at bestemme vinklen θ fra din kosinusværdi. I nogle tilfælde kan du muligvis finde vinkelværdien baseret på enhedskredsen.
   • I vores eksempel er cosθ = √2 / 2. Skriv "arccos (√2 ​​/ 2)" i din regnemaskine for at finde vinklen. En anden mulighed er at kigge efter vinklen θ på enhedskredsen, hvor cosθ = √2 / 2: dette vil være tilfældet for θ = /₄ eller 45 °.
   • Når vi samler alle oplysningerne, har vi den endelige formel θ = arccosine ((•) / (|||| || ||))

Del 2 af 2: Definition af formlen til beregning af vinklen

1. 

   Forstå formålet med formlen. Formlen, vi brugte til at beregne vinklen mellem to vektorer, var ikke afledt af allerede eksisterende regler; i stedet blev det oprettet som en definition af det skalære produkt mellem to vektorer og vinklen mellem dem. Denne beslutning er imidlertid ikke vilkårlig. Med et nærmere kig på grundlæggende geometri kan vi se, hvorfor denne formel resulterer i så nyttige og intuitive definitioner.
   • Følgende eksempler bruger todimensionelle vektorer, fordi de er den mest intuitive type at arbejde med. Vektorer med tre eller flere dimensioner har deres egenskaber defineret ud fra den generelle formel (også på en meget lignende måde).

2. 

   Gennemgå kosinusloven. I en hvilken som helst trekant skal du overveje vinklen θ dannet af siderne Det og B og siden ç modsat den vinkel. I henhold til kosinusloven er c = a + b -2ablinning(Θ). Demonstrationen af ​​denne formel kan let opnås ved viden om grundlæggende geometri.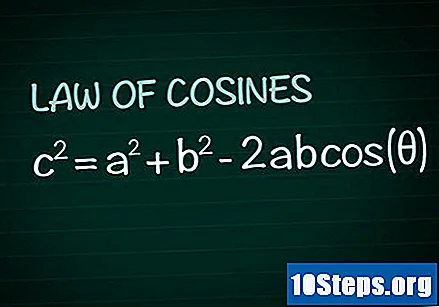

3. 

   Forbind de to vektorer for at danne en trekant. Tegn et par vektorer, og med en vinkel θ imellem dem. Tegn derefter en tredje vektor mellem dem for at danne en trekant. Med andre ord, tegne vektoren sådan, at + =, eller simpelthen = -.

4. 

   Anvend kosinusloven på denne trekant. Udskift længden på siderne på vores vektor trekant (det vil sige vektormodulet) i formlen for kosinusloven:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||linning(θ)

5. 

   Omskriv formlen ved hjælp af skalære produkter. Husk, at dot-produktet er udvidelsen af ​​en vektor, der projiceres på en anden. Det skalære produkt af en vektor i sig selv kræver ikke projektion, fordi der ikke er nogen ændring i retningen. Dette betyder, at • = || a ||. Baseret på disse oplysninger, lad os omskrive ligningen af ​​kosinusloven:
   • (-) • (-) = • + • - 2 || a || || b ||linning(θ)

6. 

   Forenkle formlen. Udvid produkterne på venstre side af ligningen og forenkle det derefter, indtil du når den formel, vi kender til beregning af vinkler.
   • • - • - • + • = • + • - 2 || a || || b ||linning(θ)
   • - • - • = -2 || a || || b ||linning(θ)
   • -2 (•) = -2 || a || || b ||linning(θ)
   • • = || a || || b ||linning(θ)

Tips

• For hurtig opløsning skal du anvende følgende formel på ethvert todimensionelt vektorpar: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Hvis du arbejder med computergrafikprogrammer, skal du sandsynligvis kun kende retningen for vektorerne, ikke deres længde. Følg nedenstående trin for at forenkle ligningerne og fremskynde dit program:
  • Normaliser hver vektor, dvs. find den enhedsvektor, der har samme retning som den originale vektor. For at gøre dette, divider hver komponent af vektoren med vektormodulet.
  • Beregn det skalære produkt af de normaliserede vektorer, ikke de originale vektorer.
  • Da modulet (det vil sige længden) for de normaliserede vektorer er enhed, kan vi lade dem ligge uden for formlen. Din endelige ligning til beregning af vinkler vil være buer (•).
• Baseret på formlen i kosinusloven kan vi hurtigt finde ud af, om den pågældende vinkel er akut eller stump. Start med cosθ = (•) / (|||| ||||):
  • Ligningens venstre og højre side skal have det samme tegn (positivt eller negativt).
  • Da længderne altid er positive, vil cosθ altid have det samme tegn som det skalære produkt.
  • Derfor, hvis det skalære produkt er positivt, vil cosθ være positiv. Dette betyder, at vinklen er i den første kvadrant af enhedskredsen, det vil sige θ <π / 2 eller 90 °. Derfor er vinklen akut.
  • Hvis det skalære produkt er negativt, er cosθ negativ. Dette betyder, at vinklen er i den anden kvadrant i enhedskredsen, det vil sige π / 2 <θ ≤ π eller 90 ° <θ ≤ 180 °. Derfor er vinklen stump.