Indhold

• Trin

I fysik er spænding den kraft, der udøves af et reb, ledning, kabel eller lignende genstand på en eller flere objekter. Alt hængende, trukket eller ophængt af et reb, kabel, ledning osv. er udsat for spænding. Som enhver kraft kan stress accelerere genstande eller forårsage deformation. At vide, hvordan man beregner stress er en vigtig færdighed ikke kun for fysikstuderende, men også for ingeniører og arkitekter, der for at garantere sikkerheden ved deres konstruktioner skal vide, om spændinger i et reb eller kabel kan modstå deformation forårsaget af genstandens vægt til at give og bryde. Følg trin 1 for at lære, hvordan man beregner stress i forskellige fysiske systemer.

Trin

Metode 1 af 2: Bestemmelse af spænding på en enkelt ledning

1. 

   
   
   Indstil kræfterne på begge sider af rebet. Spændingen i et reb er resultatet af kræfter, der trækker rebet på begge sider. For ordens skyld: "kraft = masse × acceleration". Da rebet er strakt stramt, vil enhver ændring i accelerationen eller massen af ​​genstande, der understøttes af rebet, medføre en ændring i spændingen. Glem ikke den konstante acceleration på grund af tyngdekraften: selvom et system er i balance, er dets komponenter underlagt den kraft. Vi kan tænke på spændingen i en streng som T = (m × g) + (m × a), hvor "g" er tyngdeacceleration i ethvert objekt, der trækkes af rebet, og "a" er enhver anden acceleration i de samme objekter.
   • I fysik betragter vi det som de fleste problemer som en "ideel tråd". Med andre ord er vores reb tyndt uden masse og strækker sig ikke eller knækker.
   • Lad os som et eksempel overveje et system, hvor en vægt ophænges af en træbjælke ved hjælp af et enkelt reb (se figur). Hverken vægten eller rebet bevæger sig: systemet er i balance. Vi ved, at for at vægten skal holdes i balance, skal spændingskraften være lig med tyngdekraften i vægten. Med andre ord, Spænding (F_t) = Tyngdekraft (F_g) = m × g.
     • I betragtning af en vægt på 10 kg er trækstyrken 10 kg × 9,8 m / s = 98 Newton.

2. 

   
   
   Overvej acceleration. Tyngdekraft er ikke den eneste kraft, der påvirker et rebs spænding. Enhver accelerationskraft relateret til objektet, der er fastgjort til rebet, forstyrrer resultatet. Hvis f.eks. En ophængt genstand accelereres af en kraft på rebet, føjes accelerationskraften (masse × acceleration) til spændingen forårsaget af genstandens vægt.
   • Lad os sige, at i vores eksempel på vægten på 10 kg ophængt af et reb, i stedet for at blive fastgjort på en træbjælke, bruges rebet til at hæve denne vægt til en acceleration på 1 m / s. I dette tilfælde skal vi overveje accelerationen af ​​vægten såvel som tyngdekraften og løse som følger:
     • F_t = F_g + m × a
     • F_t = 98 + 10 kg × 1 m / s
     • F_t = 108 Newton.

3. 

   
   
   Overvej rotationsacceleration. Et objekt, der roterer rundt om dets centrale punkt gennem en streng (som et pendul) udøver deformation på strengen forårsaget af centripetalkraften. Den centripetale kraft er den ekstra spændingskraft, som rebet udøver, når objektet trækkes mod midten. Således forbliver objektet i en buebevægelse, ikke i en lige linje. Jo hurtigere objektet bevæger sig, jo større er centripetalkraften. Centripetal kraft (F_ç) er lig med m × v / r, hvor "m" er masse, "v" er hastighed, og "r" er radius af cirklen, der indeholder buen, hvor objektet bevæger sig.
   • Da retningen og størrelsen af ​​den centripetale kraft ændres, når genstanden ophængt af et reb bevæger sig og ændrer hastigheden, ændres også den samlede spænding i rebet, som altid virker i den retning, der defineres af tråden, med en fornemmelse i centrum. Husk altid, at tyngdekraften konstant virker på genstanden ved at trække den ned. Så hvis et objekt roterer eller svajer lodret, er den samlede spænding større ved den nederste del af buen (for et pendul kaldes dette ligevægtspunktet), når objektet bevæger sig hurtigere og mindre i toppen af ​​buen, når det bevæger sig langsommere.
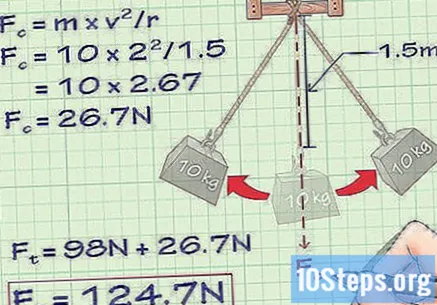
   • Lad os sige, at i vores eksempelproblem accelereres vores objekt ikke længere opad, men svinger som et pendul. Dette reb er 1,5 meter langt, og vægten bevæger sig med 2 m / s, når det passerer gennem det laveste punkt på sin bane. Hvis vi vil beregne spændingen ved det laveste punkt i buen (når den når den højeste værdi), skal vi først erkende, at belastningen på grund af tyngdekraften på dette punkt er den samme som når vægten blev suspenderet uden bevægelse: 98 Newton . For at finde den ekstra centripetale kraft, ville vi løse det som følger:
     • F_ç = m × v / r
     • F_ç = 10 × 2/1.5
     • F_ç = 10 × 2,67 = 26,7 Newton.
     • Derfor ville vores samlede spænding være 98 + 26,7 = 124,7 Newton.

4. 

   Bemærk, at spændingen på grund af tyngdekraften ændrer sig gennem buen dannet af objektets bevægelse. Som nævnt ovenfor ændrer både retningen og størrelsen af ​​den centripetale kraft, når objektet bevæger sig i sin sti. Men selv om tyngdekraften forbliver konstant, ændres "spændingen som følge af tyngdekraften" også. Når et objekt ikke er ved det laveste punkt i sin bue (dets ligevægtspunkt), trækker tyngdekraften det lige ned, men spænding trækker det op og danner en bestemt vinkel. På grund af dette skal spændingen kun neutralisere en del af tyngdekraften og ikke dens totalitet.
   • At opdele tyngdekraften i to vektorer kan hjælpe dig med at visualisere dette koncept. På et hvilket som helst punkt i buen på et objekt, der svinger lodret, danner strengen en vinkel θ med ligevægtspunktets linje og det centrale omdrejningspunkt. Når pendulet svinger, kan tyngdekraften (m × g) opdeles i to vektorer: mgsen (θ) - virker tangent til buen i retningen af ​​ligevægtspunktet; mgcos (θ), der virker parallelt med spændingskraften i den modsatte retning. Spændingen skal neutralisere mgcos (θ), den kraft, der trækker i den modsatte retning, og ikke den samlede tyngdekraft (undtagen i ligevægtspunktet, når de to kræfter er ens).
   • Lad os sige, at når vores pendul danner en vinkel på 15 grader med lodret, bevæger det sig med 1,5 m / s. Vi ville finde spænding ved at følge disse trin:
     • Stress på grund af tyngdekraften (T_g) = 98cos (15) = 98 (0,96) = 94,08 Newton
     • Centripetal kraft (F_ç) = 10 × 1,5 / 1,5 = 10 × 1,5 = 15 Newton
     • Total stress = T_g + F_ç = 94,08 + 15 = 109.08 Newton.

5. 

   Beregn friktion. Ethvert objekt, der trækkes af et reb, der har en modstandskraft, der genereres af friktionen af ​​en genstand mod en anden (eller væske), overfører denne kraft til spændingen i rebet. Friktionskraften mellem to objekter beregnes som i enhver anden situation - efter denne ligning: Kraft på grund af friktion (normalt repræsenteret af F_på) = (μ) N, hvor μ er friktionskoefficienten mellem to objekter, og N er den normale kraft mellem to objekter eller den kraft, de udøver på hinanden. Bemærk, at statisk friktion, der skyldes forsøg på at sætte et statisk objekt i bevægelse, adskiller sig fra dynamisk friktion, hvilket skyldes forsøg på at holde et objekt i bevægelse.
   • Lad os sige, at vores 10 kg-vægt ikke længere svinges, men trækkes vandret langs en flad overflade af vores reb. I betragtning af at overfladen har en dynamisk friktionskoefficient på 0,5, og vores vægt bevæger sig med en konstant hastighed, vil vi gerne accelerere den til 1 m / s. Dette nye problem præsenterer to vigtige ændringer: For det første behøver vi ikke længere beregne spændingen på grund af tyngdekraften, fordi vægten ikke suspenderes af rebet. For det andet skal vi beregne spændingen forårsaget af friktion såvel som den, der skyldes accelerationen af ​​massen af ​​den vægt. Vi skal løse følgende:
     • Normal kraft (N) = 10 kg × 9,8 (tyngdeacceleration) = 98 N
     • Dynamisk friktionskraft (F_atd) = 0,5 × 98 N = 49 Newton
     • Accelerationskraft (F_Det) = 10 kg × 1 m / s = 10 Newton
     • Total stress = F_atd + F_Det = 49 + 10 = 59 Newton.

Metode 2 af 2: Beregning af multipel strengstress

1. 

   Træk ophængte laster lodret og parallelt ved hjælp af en remskive. Remskiver er enkle maskiner, der består af en ophængt skive, der gør det muligt for spændingskraften at ændre retning. I en simpel remskivekonfiguration løber rebet eller kablet langs remskiven med vægte fastgjort til begge ender og skaber to segmenter reb eller kabel. Imidlertid er spændingen i begge ender af rebet den samme, selvom de trækkes af kræfter af forskellig størrelse. I et system med to masser ophængt af en lodret remskive er spændingen lig med 2g (m₁) (m₂) / (m₂+ m₁), hvor "g" er tyngdeacceleration, "m₁"er massen af ​​objekt 1, og" m₂"er massen af ​​objekt 2.
   • Bemærk, at fysiske problemer generelt betragter "ideelle remskiver": uden masse uden friktion, som ikke kan knække, deformere eller løsne sig fra loftet eller rebet, der ophænger det.
   • Lad os sige, at vi har to vægte, der er ophængt lodret fra en remskive ved hjælp af parallelle reb. Vægt 1 har en masse på 10 kg, mens vægt 2 har en masse på 5 kg. I dette tilfælde finder vi spændingen sådan:
     • T = 2 g (m₁) (m₂) / (m₂+ m₁)
     • T = 2 (9,8) (10) (5) / (5 + 10)
     • T = 19,6 (50) / (15)
     • T = 980/15
     • T = 65.33 Newton.
   • Bemærk, at fordi en vægt er tungere end en anden, og alle andre ting er ækvivalente, vil dette system accelerere med vægten på 10 kg, der bevæger sig nedad, og vægten på 5 kg bevæger sig opad.
2. Foretag beregninger for belastninger ophængt af en remskive med ikke-parallelle lodrette reb. Remskiver bruges ofte til at dirigere spændinger i en retning snarere end op eller ned. Hvis for eksempel en vægt er ophængt lodret på den ene ende af rebet, mens den anden ende er forbundet med en anden vægt på en diagonal hældning, har det ikke-parallelle remskivesystem form af en trekant med punkter på den første og anden vægt og remskive. I dette tilfælde påvirkes spændingen i rebet både af tyngdekraften i vægten og af den komponent af kraften, der er parallel med rebets diagonale sektion.
   • Lad os sige, at vi har et system med en vægt på 10 kg (m₁) ophængt lodret og forbundet gennem en remskive til en vægt på 5 kg (m₂) på en 60 graders rampe (forudsat at rampen ikke har nogen friktion). For at finde spændingen i strengen er det lettere at finde ligningerne for de kræfter, der accelererer vægtene først. Følg disse trin:
     • Den ophængte vægt er tungere, og vi overvejer ikke friktion; derfor ved vi, at det vil accelerere nedad. På trods af spændingen i rebet, der trækker vægten op, accelererer systemet på grund af den resulterende kraft F = m₁(g) - T eller 10 (9.8) - T = 98 - T.
     • Vi ved, at vægten på rampen vil accelerere opad. Da rampen ikke har nogen friktion, ved vi, at spændingen trækker dig op ad rampen og "kun" din egen vægt trækker den ned. Den nedadgående kraftkomponent er givet af mgsen (θ), så i vores tilfælde kan vi ikke sige, at den accelererer op ad rampen på grund af den resulterende kraft F = T - m₂(g) sen (60) = T - 5 (9,8) (0,87) = T - 42,14.
     • Accelerationen af ​​de to vægte er ækvivalent. Så vi har (98 - T) / m₁ = (T - 42,63) / m₂. Efter et trivielt job for at løse ligningen når vi frem til resultatet af T = 60,96 Newton.

3. 

   Overvej flere strenge, når du løfter en vægt. Lad os endelig overveje et objekt, der er ophængt i et strengsystem i form af en Y: to strenge fastgjort til loftet, som er i et centralt punkt, hvor en vægt er ophængt af en tredje streng. Spændingen i den tredje streng er indlysende: det er simpelthen den spænding, der skyldes tyngdekraften, eller m (g). De resulterende spændinger i de to andre strenge er forskellige og skal have en sum lig med tyngdekraften med lodret retning opad og lig med nul i begge vandrette retninger, forudsat at systemet er i ligevægt. Spændingen i strengene påvirkes både af massen af ​​den ophængte genstand og vinklen, hvorved hver streng er i loftet.
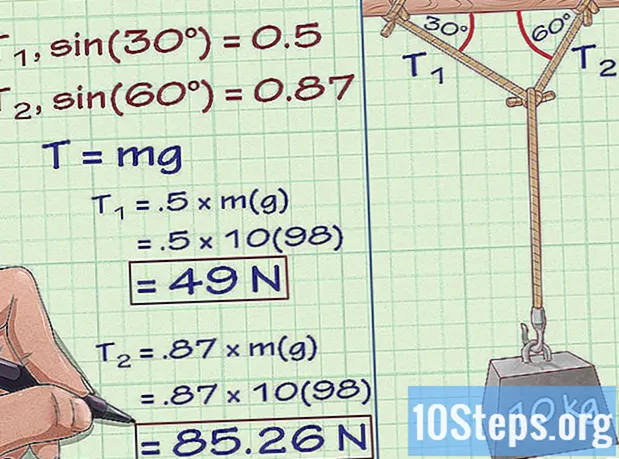
   • Lad os sige, at i vores Y-formede system har bundvægten en masse på 10 kg, og de to øverste strenge mødes i loftet i en vinkel på henholdsvis 30 og 60 grader. Hvis vi vil finde spændingen i hver af de øverste strenge, bliver vi nødt til at overveje de lodrette og vandrette komponenter i hver spænding. I dette eksempel er de to strenge stadig vinkelrette på hinanden, hvilket gør det let at beregne i henhold til definitionerne af følgende trigonometriske funktioner:
     • Forholdet mellem T = m (g) og T.₁ eller T₂ og T = m (g) er lig med sinus for vinklen mellem hvert støttetov og loftet. For dig₁, sinus (30) = 0,5, og for T₂, sinus (60) = 0,87
     • Multiplicer spændingen i den nederste streng (T = mg) med sinus for hver vinkel for at finde T₁ og T₂.
     • T₁ = 5 × m (g) = 5 × 10 (9,8) = 49 Newton.
     • T₁ = 87 × m (g) = 87 × 10 (9,8) = 85.26 Newton.